Az első olvasás alkalmával nem hittem a szememnek, második olvasatra azt hittem, hogy egy „másik” Napóleonról van szó, aztán álmélkodva konstatáltam, hogy igen, a nagy francia hadvezér a matematika birodalmában is „otthagyta az ujjlenyomatát”. 😊
A Wikipédiában ez található Napóleon matematikai munkásságával kapcsolatban:
| A külső Napóleon-háromszögre vonatkozó tétel Ha az ABC háromszög oldalaira kifelé emelünk egy-egy szabályos háromszöget, akkor e szabályos háromszögek középpontjai mindig szabályos háromszöget alkotnak. Ezt a szabályos háromszöget az eredeti háromszöghöz tartozó külső Napóleon-háromszögnek nevezzük. A belső Napóleon-háromszögre vonatkozó tétel Ha az ABC nem egyenlő oldalú háromszög oldalaira befelé emelünk egy-egy szabályos háromszöget, akkor e szabályos háromszögek középpontjai mindig szabályos háromszöget alkotnak. (Ha az ABC háromszög egyenlő oldalú, akkor az oldalaira befelé szerkesztett szabályos háromszögek középpontjai egy pontba esnek és nem alkotnak háromszöget.) Ezt a szabályos háromszöget az eredeti háromszöghöz tartozó belső Napóleon-háromszögnek nevezzük. | 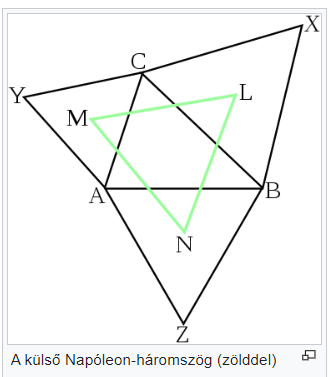 |
A külső és a belső Napóleon-háromszög területére vonatkozó tétel
Tekintsük egy háromszög külső és belső Napóleon-háromszögének területét. A háromszöghöz tartozó külső és belső Napóleon-háromszög területének különbsége egyenlő az eredeti háromszög területével. Egyenlő oldalú ABC háromszög külső Napóleon-háromszöge egybevágó az eredeti ABC háromszöggel, azaz azzal egyenlő területű, a belső Napóleon háromszög pedig egy ponttá fajult, vagyis területe 0, tehát az egyenlő oldalú háromszögre is érvényes a Napóleon háromszögek területére vonatkozó tétel.
